NIC Excellence Project 2017/1
Numerische Untersuchungen von Strukturen und Phasen in (Nano-)Systemen in eingeschränkter Geometrie

John von Neumann Exzellenzprojekt 2017
Prof. Peter Nielaba, Universität Konstanz
In diesem Projekt wurden auf JURECA Computersimulationen von Vielteilchensystemen durchgeführt. Die untersuchten Systeme (Kolloide, Nanodrähte, Fluide, Kristallite) und Fragestellungen (Strukturbildungen, Transport, Phasenumwandlungen) sind dabei von Bedeutung für die Konstanzer Sonderforschungsbereiche SFB 767 und SFB 1214.
In den letzten Jahren hat sich der Trend zu immer kleineren und leistungsfähigeren elektronischen Bauelementen fortgesetzt, die wir im Alltag in den modernen Smartphones und Laptops realisiert sehen, die aber auch in Großrechnern für wissenschaftliche Untersuchungen von immenser Bedeutung sind. In diesem Zusammenhang stellt sich die Frage, bis zu welchen minimalsten Größenordnungen man überhaupt noch von Drähten sprechen kann, die elektronische Bauelemente kontaktieren, und welche physikalischen Phänomene dort relevant sind. Sicher wird auf kleinsten Längenskalen die Quantenmechanik wichtig werden, die in klassischen Überlegungen unberücksichtigt bleibt. Darüber hinaus stellt sich die Frage, was denn der Querschnitts-Grenzwert für kleinstmögliche Drähte ist. Ein Draht aus einer linearen Anordnung von Atomen ist hier die Antwort. In der Realität gibt es nur wenige Materialien, die eine atomare Drahtstruktur in Form einer Kette aufweisen. Das wichtigste Beispiel ist ein atomarer Draht aus Gold-Atomen [1], daneben gibt es auch (kurze) atomare Platin-Drähte. Diese Materialien bilden bei einem kontinuierlichen Auseinanderziehen in Drahtrichtung sogenannte „atomare Nanodrähte“ aus. Die Phänomene beim Ausbilden atomarer Drähte lassen sich in diesen Materialien darauf zurückführen, dass die atomaren Bindungen zwischen zwei benachbarten Teilchen in einer linearen Anordnung aus relativistischen Gründen energetisch günstiger sind als im Falle einer regulären Ausrichtung im Festkörper.
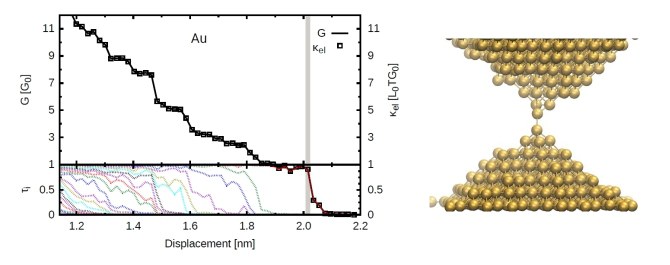
Metalle, die den elektrischen Strom gut leiten, transportieren Wärme in der Regel ähnlich gut. In beiden Fällen wird die Energie maßgeblich durch die gleichen Teilchen – frei bewegliche Elektronen – übertragen. Legt man zwischen den Enden eines metallischen Drahtes eine Spannung an, so fließt ein elektrischer Strom, ein Ladungstransport findet statt. Dabei heizt sich der Draht nicht nur auf, sondern mit der Bewegung der Ladungsträger ist auch ein Energie- oder Wärmetransport verbunden, ein sogenannter Wärmestrom. Zwischen dem Ladungstransport und dem Wärmetransport in Metallen besteht ein Zusammenhang, der in Form des empirischen Wiedemann-Franz-Gesetzes formuliert werden kann. Dabei beschreibt man die Transportphänomene durch die Größen „Wärmeleitfähigkeit“ κ und „elektrische Leitfähigkeit“ G, und das Wiedemann-Franz-Gesetz besagt, dass - unabhängig vom betrachteten Metall - κ =L0TG ist, wobei T die Temperatur und L0 die Lorenz-Zahl ist. Letztere ergibt sich in einer klassischen Modellierung im Rahmen des Drude-Sommerfeld-Modelles als L0 =π2 kB2/(3e2), wobei kB die Boltzmannkonstante und e die Elementarladung ist.
Atomare Drähte eignen sich nun hervorragend dazu, eine Analyse des elektrischen Transportes und des Wärmetransportes auf atomarer Längenskala durchzuführen. Eine experimentelle Untersuchung dieser Phänomene ist aufwändig und erst jetzt möglich geworden [2] (in den Experimentalgruppen von E. Meyhofer und P. Reddy, U. Michigan (USA)), wobei unsere theoretische Modellierungen und Berechnungen wegweisend waren [2] (mit M. Matt, J. C. Klöckner, F. Pauly und J. C. Cuevas). Der Wärmetransport in atomaren Nanodrähten ist dabei sowohl durch Atomschwingungen, als auch durch die Bewegung von Elektronen bestimmt. Beide Komponenten müssen quantenmechanisch berechnet werden.
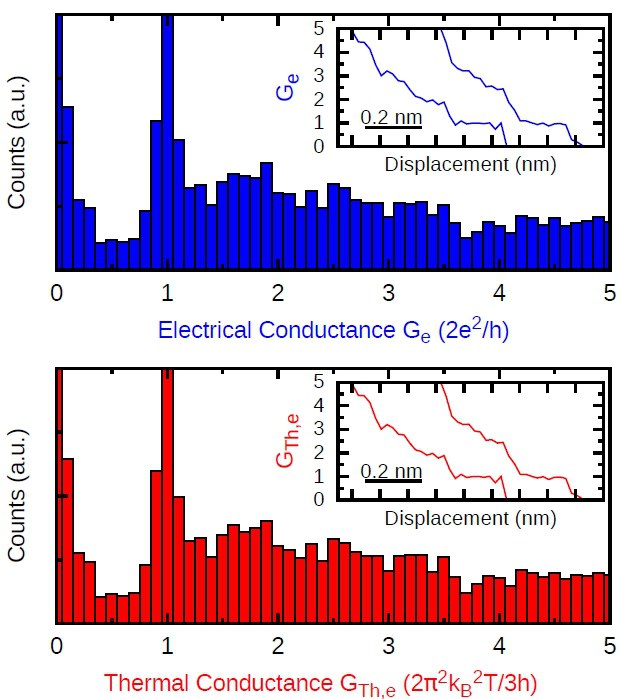
Damit wurde eine Überprüfung des Wiedemann-Franz-Gesetzes, das ja einen Beitrag der Gitterschwingungen auf die thermische Leitfähigkeit vernachlässigt, auch auf der Nanometer-Längenskala möglich. Da es sich um einen empirischen Zusammenhang handelt, würde man vielleicht zunächst vermuten, dass auf atomarer Skala kein Grund für eine derartige Beziehung bestehen sollte, da alle relevanten Größen quantisiert sind. Die elektrische Leitfähigkeit zum Beispiel wird in Einheiten des Leitwertquantums G0=2e2/h angegeben mit dem Planck’schen Wirkungsquantum h. Tatsächlich zeigt sich in einem Vergleich von experimentellen und theoretischen Studien [2], dass das Wiedemann-Franz-Gesetz auch für atomare Gold- und Platin-Drähte Gültigkeit hat. Bei der Untersuchung dieses Zusammenhanges wurden nicht nur einzelne Ziehvorgänge analysiert (s. Abb.1), sondern mit umfangreichen statistischen Ensemblesimulationen auch Histogramme der elektrischen Leitfähigkeit und der Wärmeleitfähigkeit bestimmt und miteinander verglichen (s. Abb.2), wobei die Korrelationen einen eindeutigen Zusammenhang im Sinne des Wiedemann-Franz-Gesetzes ergeben.
Ob sich diese Erkenntnisse auch auf andere Materialien übertragen lassen oder ob es Abweichungen vom Wiedemann-Franz-Gesetz gibt, oder welche anderen interessanten Effekte den Transport auf atomarer Längenskala beeinflussen, wird sich in weiteren spannenden Studien zeigen (mit F. Müller und M. Ring).
Darüber hinaus wurden in kolloidalen Systemen in zweidimensionaler Kanalgeometrie und einem externen sinusförmigen Potential interessante Transportphänomene analysiert [3] (mit U. Siems). Durch das externe periodische Potential wird eine Lagenordnung und die Gleichgewichtsstruktur gestört, und in Abhängigkeit der Kommensurabilität der Gitterperiodizität mit der Periodizität des externen Potentials ergeben sich Veränderungen der Mobilität. So treten zum Beispiel unter der Einwirkung einer externen konstanten Kraft in Kanalrichtung auf die Teilchen sogenannte Kinks und Anti-Kinks auf, bei denen sich lokal entweder n+1 oder n-1 Teilchen n Potentialminima teilen müssen, und sich diese "Quasiteilchen" im Falle der Kinks in Richtung der Kraft bewegen, und die Anti-Kinks in die entgegengesetzten Richtung. Darüber hinaus kann die Diffusion aufgrund einer rascheren Dynamik der Teilchen an den Kanalwänden um mehrere Größenordnungen erhöht sein. Auswirkungen von Gegenströmungen auf Strukturbildungen werden derzeit untersucht.
Quencht man ein Fluid durch Temperaturveränderung in ein Entmischungsgebiet, so entwickeln sich die Komponenten zeitlich so, dass im Langzeitlimes die Binodalen erreicht werden. Für die zeitliche Entwicklung bei der spinodalen Entmischung gibt es in erster Linie für einen späten Zeitbereich theoretische Aussagen zur Zeitentwicklung des Domänenwachstums. Experimentell sind die frühen Zeitbereiche nur schwer zugänglich, da der Quench nicht instantan realisiert werden kann und daher unterschiedliche Zeitbereiche der Entmischung und des Quench-Prozesses gleichzeitig auftreten, darüber hinaus sind in der Regel auch gravitative Effekte zu beachten. Durch Verwendung und Modifikation [4] (mit M. Pütz) des in der Astrophysik u.a. bei der Modellierung von Galaxien [5] (mit M. Beck und der Gruppe von K. Dolag, München) verwendeten Verfahrens der "smoothed particle hydrodynamics" konnte nun unter Berücksichtigung der Hydrodynamik eine Überbrückung der auftretenden Zeitskalen erzielt werden [4], wobei auch ein Zwischenbereich zwischen der frühen und späten Phase analysiert werden konnte, so dass nun ein leistungsfähiges Verfahren zur Behandlung von Fluid-Systemen unter Berücksichtigung der Hydrodynamik vorliegt, das z.B. für die Behandlung kolloidaler Systemen in externen Feldern von Bedeutung ist.
Weitere Studien zur Nukleation und zum Kristallwachstum (mit R. Schmid) und zu Nanoresonatoren (mit C. Scholz) befinden sich in einem fortgeschrittenen Projektstadium.
Literaturverweise:
[1] M. Dreher, F. Pauly, J. Heurich, J. C. Cuevas, E. Scheer, P. Nielaba, Phys. Rev. B 72, 075435 (2005).
[2] L. Cui, W. Jeong, S. Hur, M. Matt, J. C. Klöckner, F. Pauly, P. Nielaba, J. C. Cuevas, E. Meyhofer, P. Reddy, Science 355, 1192 (2017).
[3] U. Siems, P. Nielaba, Phys. Rev. E 91 , 022313 (2015).
[4] M. Pütz and P. Nielaba, Phys. Rev. E 94, 022616 (2016).
[5] M. C. Beck, A. M. Beck, R. Beck, K. Dolag, A. W. Strong, P Nielaba, JCAP, 05, 056 (2016).
Kontakt:
Prof. Peter Nielaba, Universität Konstanz
peter.nielaba@uni-konstanz.de





