NIC Excellence Project 2022/1
Turbulente Konvektion: Wie entsteht Ordnung auf der Mesoskala?

John von Neumann Exzellenzprojekt 2022
Prof. Jörg Schumacher (TU Ilmenau)
Turbulente, thermisch getriebene Konvektionsströmungen in der Natur erstrecken sich typischerweise über einen großen Bereich von Längen und Zeiten, die von (vielen) tausenden Kilometern bis zu Zentimetern und von Tagen bis zu Sekunden reichen. Im mittleren Längenbereich, den sogenannten Mesoskalen, ist die Strömung oft in nahezu regulären und teilweise sogar hierarchischen Mustern organisiert. Ein prominentes Beispiel ist das optisch beobachtbare wabenförmige Netzwerk der Granulen und die mittels Helioseismologie detektierbaren darunter liegenden Supergranulen in der oberen Konvektionszone der Sonne [1].
Wie entsteht diese Ordnung in einer hochgradig turbulenten und chaotischen Strömung? In den vergangenen Jahren sind wir dieser Frage mittels numerischer Simulationen der zu Grunde liegenden nichtlinearen Strömungsgleichungen in einer vereinfachten fundamentalen Strömung, der Rayleigh-Bénard-Konvektion, nachgegangen. Der Parameter, der den Antrieb der Turbulenz charakterisiert, ist die Rayleighzahl. Im Rayleigh-Bénard-System wird eine Flüssigkeitsschicht gleichmäßig von unten beheizt und oben gekühlt. Ist der resultierende Temperaturunterschied stark genug, kann die Wärme nicht mehr allein durch Diffusion von unten nach oben transportiert werden. Bei einer exakt berechenbaren Rayleighzahlschwelle setzt zusätzlich eine Flüssigkeitsbewegung in der Schicht ein, die die Wärme effektiver abführt. Wächst die Rayleighzahl weiter, wird die Strömung turbulent.
Unsere numerischen Simulationen zeigten erstmals, dass die thermischen Randbedingungen einen entscheidenden Einfluss auf die Mesoskalenordnung haben. Im Falle eines am oberen und unteren Rand vorgegebenen Wärmestroms formiert sich in der Rayleigh-Bénard-Turbulenz langsam eine große Konvektionszelle, eine Supergranule, die von einem feineren Granulenmuster überlagert ist (siehe Abbildung). Das Bestreben der Strömung, mit einer großen Zelle das Strömungsvolumen zu füllen, wird für den Einsatzpunkt der Konvektion vorhergesagt. Unsere Simulationen konnten nun zeigen, dass selbst die vollständig turbulente Strömung bei großen Rayleighzahlen ihren Ursprungsmechanismus noch nicht „vergessen“ hat [2].
Konvektive Turbulenz in natürlichen Systemen, wie im Inneren der Sonne, erfüllt die vereinfachenden Annahmen des Rayleigh-Bénard-Falls nicht. Die Dichte als thermodynamische Zustandsgröße ändert sich beispielsweise um Größenordnungen über die gesamte Konvektionsschicht, besonders stark nahe der Oberfläche. Deren Berücksichtigung erfordert die Erweiterung der Modellgleichungen auf den kompressiblen Strömungsfall, dem wir im vorliegenden Exzellenzprojekt nachgehen möchten. Da die maximale Strömungsgeschwindigkeit nun in den Bereich der Schallgeschwindigkeit des Mediums und darüber hinaus reichen kann, muss auch die numerische Methode zur Simulation adaptiert werden. In kompressiblen Strömungen variiert die Dichte des Fluids und ruft somit zusätzliche Instabilitäten bzw. qualitativ neue Strukturen, wie lokale Dichtesprünge, hervor. Deren Einfluss auf die Mesoskalenmuster und die fluktuierenden kleinskaligen Wirbel sowie auf den turbulenten Wärmetransport durch die Konvektionsschicht soll hier aufgeklärt werden. Die vom John von Neumann Institut für Computing auf den JUWELS Cluster- und Booster-Systemen bewilligte Rechenzeit ermöglicht uns, diese komplexeren Konvektions- und Strukturbildungsprozesse systematisch zu untersuchen und die aufgeworfene Frage nach dem Ursprung der Ordnung auf der Mesoskala zu beantworten.
Literatur
[1] J. Schumacher und K.R. Sreenivasan, Rev. Mod. Phys. 92, 041001 (2020).
[2] P.P. Vieweg, J.D. Scheel und J. Schumacher, Phys. Rev. Res. 3, 013231 (2021).
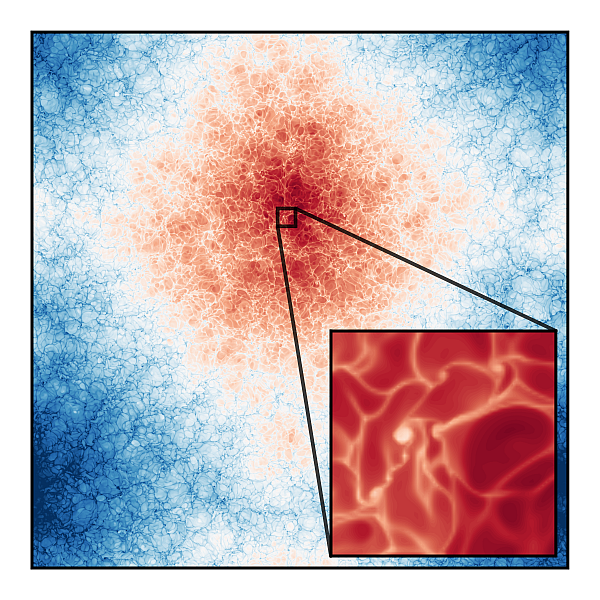
Draufsicht auf eine turbulente Konvektionsschicht, die durch einen konstanten Wärmestrom getrieben wird. Schon in der idealisierten Rayleigh-Bénard-Strömung formiert sich dann langsam eine hierarchische Ordnung. Sie besteht aus einer Supergranule (rote Zelle in der Bildmitte), die von einem feinen Granulennetzwerk (siehe Vergrößerung rechts unten) überlagert wird
Copyright: Prof. Jörg Schumacher, TU Ilmenau





