NIC Excellence Project 2024/1

Neural Wave Functions for Materials Physics

_{John von Neumann Excellence Project 2024/1
Prof. Johannes Knolle (Technische Universität München)}

The unitary Fermi gas is a paradigmatic example of a strongly interacting system of two-component fermions which possesses superfluid ground states. It is an effective description of a wide spectrum of strongly correlated fermionic systems, from macroscopic examples such as neutron matter in the inner crust of a neutron star, to microscopic examples such as ultracold Fermi gases. A great deal of effort has been put into studying the unitary Fermi gas over the past few decades, but a full quantitative understanding has not yet been achieved and remains a grand challenge in many-body physics.

With recent advances in deep learning algorithms, neural-network-based approaches have permeated most areas of computational physics, including lattice and continuum quantum Monte Carlo simulations. The group of Prof. Foulkes, which is actively involved in the project, has been among the pioneers in the field since they introduced the Fermionic Neural Network (FermiNet) [D. Pfau et al., Phys. Rev. Research, 2, 033429 (2020)]. They achieved state-of-the-art results for various atoms and molecules and our FermiNet paper has received over 500 citations since 2020. They also generalised the method to the homogeneous electron gas and solids with great success.

In a recent collaborative work with the group of Prof. Knolle [Wan Tong Lou, et al., Phys. Rev. X 14, 021030 (2024)], it was shown that the original FermiNet architecture fails both quantitatively and qualitatively to describe Cooper pairing in the unitary Fermi gas. This is the first time that FermiNet fails, but the problem can easily be remedied. The original FermiNet replaced the one-particle orbitals in Hartree-Fock theory by many-particle generalizations. The PhD student Wan Tong Lou generalised the fixed-particle number BCS (AGPs) wavefunction in an analogous way, producing what they called an AGPs FermiNet. This leads to substantial improvements in the accuracy of the results despite the use of fewer variational parameters than the original FermiNet. It outperforms state-of-the-art fixed-node diffusion Monte Carlo calculations [M. M. Forbes et al., Phys. Rev. Lett., 106, 235303 (2011)] and produces various quantities related to a superfluid, such as the pairing gap and the superfluid condensate fraction, in good agreement with experiments and previous simulations.

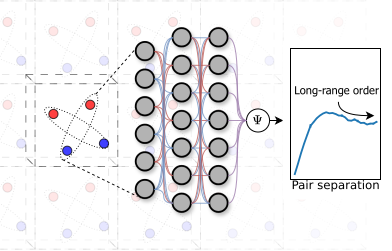
As the first neural-network approach to study fermionic superfluids in the continuum, the approach has several advantages over previous QMC methods: the use of a neural network removes the need for an underlying basis set; and the flexibility of the network yields extremely accurate results within a variational Monte Carlo framework that provides access to unbiased estimates of arbitrary ground-state expectation values. Based on this collraborative work and the previous prediction of the quantum phase transition in the homogeneous electron gas using FermiNet with no a priori knowledge of the transition [G. Cassella et al., Phys. Rev. Lett., 130, 036401 (2023)], we believe that our architecture can be easily applied to study other more exotic superfluids and may be able to predict unknown quantum phases in these systems.